The Three-Phase Journey
mimicry analyzes
mimicry observes your running system and learns what it actually does - millions of transactions, thousands of rules, every edge case. Works even when source code is unavailable or subject matter experts have left.
You understand
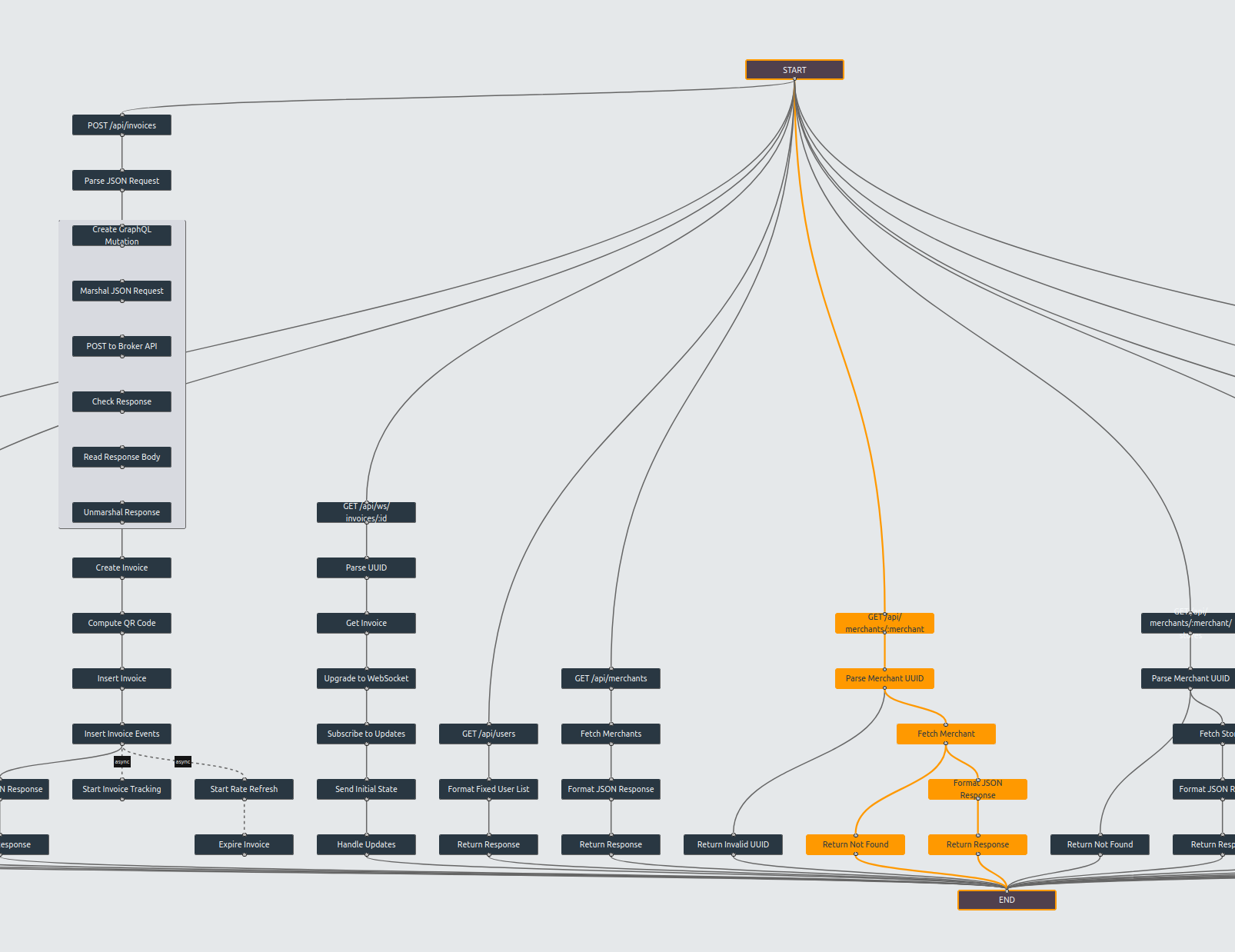
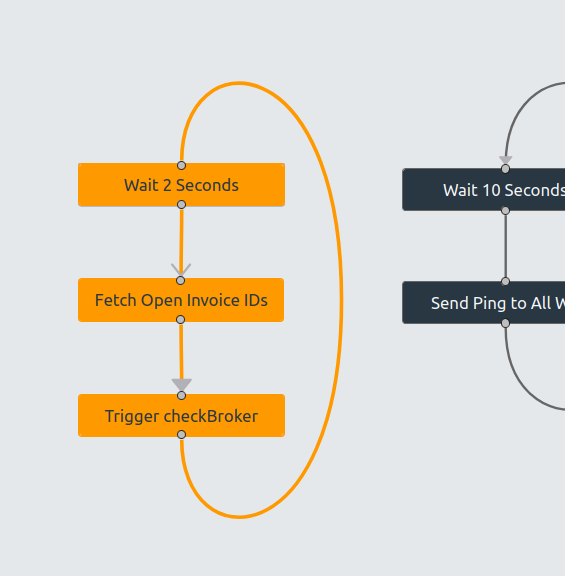
Within weeks, you get an interactive atlas of your real system behavior. Zoom from complete workflows down to individual business rules. See the full dataflow or trace a single transaction through the system. Finally see both forest and trees.
Then change
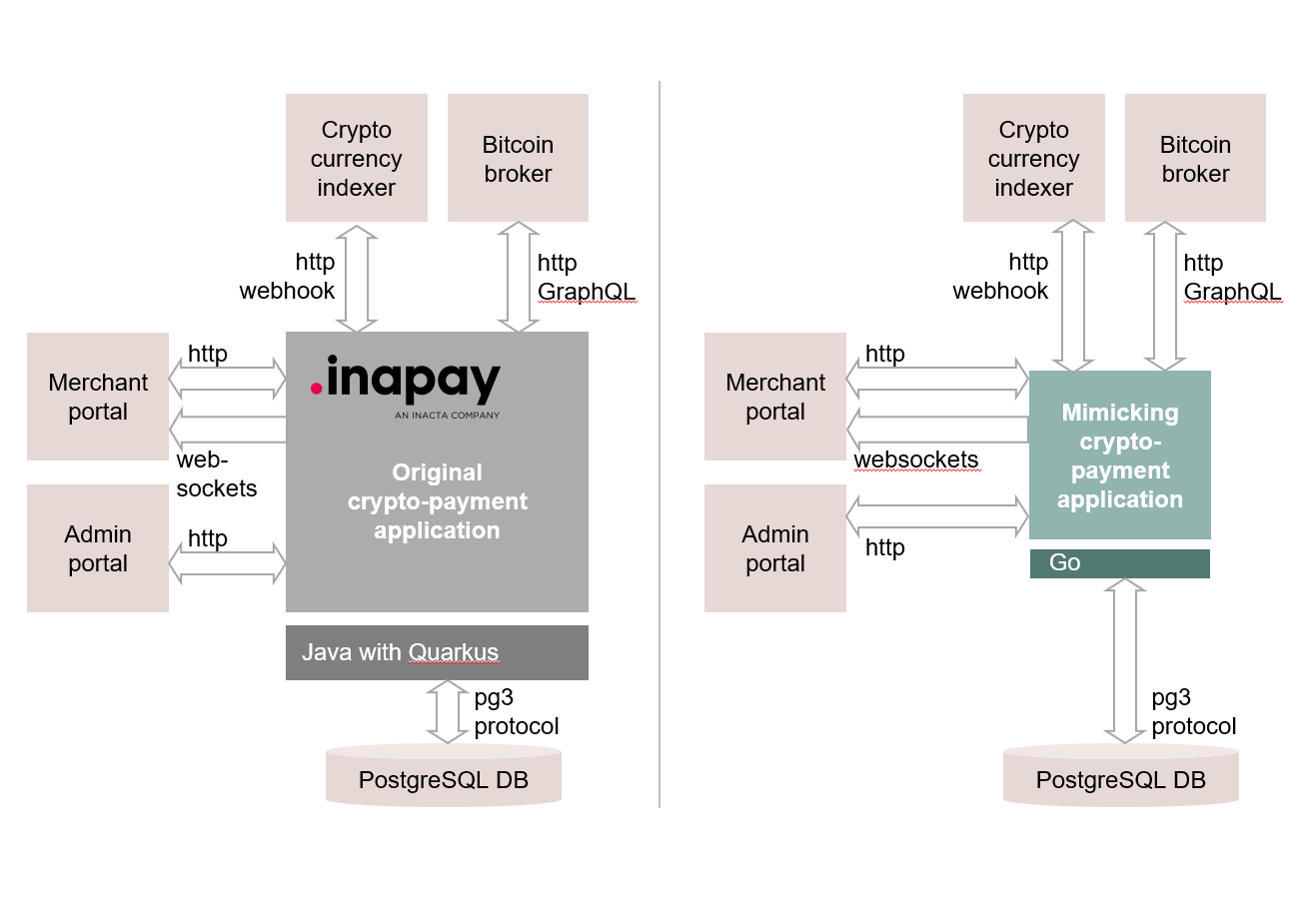
We deliver an executable specification - a validated, working system in a modern architecture that behaves equivalently to your legacy application. Not built from scratch - derived from what mimicry learned. Same inputs, same outputs, same business rules, but on technology where development is fast again.
The system perfectly reflects the analysis results, giving you complete documentation with direct links between code and behavior. Use it as your new system, adapt it to your specific architecture, or treat it as blueprints for your team. You own it. You decide what’s next.